Widerstände werden überall dort verwendet, wo die vorliegende Spannung für ein Bauteil zu hoch ist. Ist beispielsweise die Nennspannung einer Leuchtdiode mit 3 V angegeben, so würde diese zerstört werden, wenn man sie direkt an eine 9 V-Batterie anschließt.
Angenommen die Nennstromstärke der Leuchtdiode beträgt 48 mA, dann kann man die Größe des benötigten Vorwiderstands wie folgt berechnen:
\[ R = \frac{U}{I} = \frac{9 V – 6 V }{ 0,048 A} = 125 \Omega \]
Problem: Es gibt keinen $\color{red}{125 \Omega}$-Widerstand zu kaufen. Nirgends. Kein Hersteller dieser Welt produziert einen $\color{red}{125 \Omega}$-Widerstand.
Verwendet man einen Widerstand, der kleiner ist als $125 \Omega$, besteht die Gefahr, dass die LED trotzdem zerstört wird. Verwendet man einen größeren Widerstand kann es sein, dass die LED nicht ausreichend hell leuchtet.
Um nun trotzdem einen $125 \Omega$-Widerstand ersetzen zu können und die LED optimal betreiben zu können, liegt es nahe, die Reihen- und Parallelschaltung von Widerständen zu untersuchen.
Reihenschaltung von Widerständen
Experimentelle Untersuchung der Reihenschaltung von Widerständen
Die experimentelle Untersuchung der Reihenschaltung von Widerständen gestaltet sich experimentell einfach: Wir schalten beliebig viele Widerstände in Reihe und messen mit einem Multimeter direkt den Gesamtwiderstand der Schaltung. Der Einfachheit halber untersuchen wir in einem ersten Schritt zunächst die Reihenschaltung mehrer gleich großer Widerstände ($100 \Omega$ und erst in einem zweiten Schritt zwei verschieden große Widerstände.
| Anzahl | Gesamtwiderstand in $\Omega$ |
| 1 | 100 |
| 2 | 200 |
| 3 | 300 |
| 4 | 400 |
| 5 | 500 |
| Widerstand 1 in $\Omega$ | Widerstand 2 in $\Omega$ | Gesamtwiderstand in $\Omega$ |
| 100 | 500 | 600 |
| 100 | 50 | 150 |
| 50 | 500 | 550 |
| 1000 | 500 | 1500 |
| 50 | 1000 | 1050 |
Man erkennt leicht einen Zusammenhang:
In einer Reihenschaltung ist der Gesamtwiderstand gleich der Summe der Einzelwiderstände oder als Formel geschrieben:
\[ \boxed{R_{ges}=R_1+R_2} \]
Entsprechend gilt auch für mehrere Widerstände
\[ \boxed{R_{ges}=R_1+R_2+R_3+\dots} \]
Insbesondere steigt also der Gesamtwiderstand einer Schaltung, wenn ein weiterer Widerstand in Reihe geschaltet wird.
Theoretische Herleitung einer Formel für die Reihenschaltung von Widerständen
benötigtes Vorwissen
Experimentell ist die Formel bestätigt. Es folgt die theoretische Bestätigung mit Hilfe von Vorwissen. Konkret wissen, muss man für eine vollständige theoretische Herleitung der Formel:
Wie verhält sich die Spannung in einer Reihenschaltung? Es gilt $U_{ges}=U_1+U_2$, die Teilspannungen ergeben also zusammen die Gesamtspannung.
Wie verhält sich die Stromstärke in einer Reihenschaltung? Die Stromstärke ist in einer Reihenschaltung überall gleich groß, es ist also $I_{ges}=I_1=I_2$.
Wie lautet die Definition für den elektrischen Widerstand? Der elektrische Widerstand $R$ wird definiert als $R=\frac{U}{I}$.
theoretische Herleitung
Da die Spannung in einer Reihenschaltung immer gleich bleibt, gilt:
\[U_{ges}=U_1+U_2 \]
Mit Hilfe der Definition des elektrischen Widerstands können wir jedes $U$ in obiger Gleichung ersetzen durch $R\cdot I$, also:
\[R_{ges}\cdot I_{ges} = R_1\cdot I_1 + R_2\cdot I_2 \]
In einer Reihenschaltung ist die Stromstärke überall gleich, also können wir $I_{ges}$, $I_1$ und $I_2$ einfach durch $I$ ersetzen.
\[R_{ges}\cdot I = R_1\cdot I+ R_2\cdot I \]
Letzter Schritt: Wir können die gesamte Gleichung durch $I$ teilen und erhalten die schon vermutete Formel:
\[\boxed{R_{ges} = R_1+ R_2}\]
Parallelschaltung von Widerständen
Experimentelle Untersuchung der Parallelschaltung von Widerständen
Auch bei der experimentellen Untersuchung der Parallelschaltung von Widerständen können wir die Messung einfach mit einem Multimeter durchführen, konzentrieren uns hier aber auf die Untersuchung gleich großer Widerstände ($100 \Omega$), da der Zusammenhang bei verschieden großen Widerständen so komplex ist, dass man diesen aus den Messwerten nicht unmittelbar erkennen könnte. Hier hilft dann später die theoretische Herleitung.
| Anzahl | Gesamtwiderstand in $\Omega$ |
| 1 | 100 |
| 2 | 50 |
| 3 | 33,3 |
| 4 | 25 |
| 5 | 20 |
| 6 | 16,7 |
Auch hier lässt sich ein Zusammenhang erkennen. Offenbar ergibt sich der Gesamtwiderstand der Parallelschaltung gleich großer Widerstände, indem man die Größe eines einzelnen Widerstands durch die Größe eines einzelnen Widerstands teilt.
\[ \boxed{ \text{Gesamtwiderstand} = \frac{\text{Größe eines einzelnen Widerstands}}{\text{Anzahl der Widerstände }} }\]
Für verschieden große Widerstände, ist die theoretische Herleitung nötig:
Theoretische Herleitung einer Formel für die Parallelschaltung von Widerständen
benötigtes Vorwissen
Experimentell ist die Formel bestätigt. Es folgt die theoretische Bestätigung mit Hilfe von Vorwissen. Konkret wissen, muss man für eine vollständige theoretische Herleitung der Formel:
Wie verhält sich die Stromstärke in einer Parallelschaltung? Es gilt $I_{ges}=I_1+I_2$, die Teilstromstärken ergeben also zusammen die Gesamtstromstärke.
Wie verhält sich die Spannung in einer Parallelschaltung? Die Spannung ist in einer Parallelschaltung überall gleich groß, es ist also $U_{ges}=U_1=U_2$.
Wie lautet die Definition für den elektrischen Widerstand? Der elektrische Widerstand $R$ wird definiert als $R=\frac{U}{I}$.
theoretische Herleitung
Da die Stromstärke in einer Reihenschaltung immer gleich bleibt, gilt:
\[I_{ges}=I_1+I_2 \]
Mit Hilfe der Definition des elektrischen Widerstands können wir jedes $I$ in obiger Gleichung ersetzen durch $\frac{U}{R}$, also:
\[\frac{U_{ges}}{R_{ges}} = \frac{U_1}{R_1} + \frac{U_2}{R_2} \]
In einer Parallelschaltung ist die Spannung überall gleich, also können wir $U_{ges}$, $U_1$ und $U_2$ einfach durch $U$ ersetzen.
\[\frac{U}{R_{ges}} = \frac{U}{R_1} + \frac{U}{R_2} \]
Letzter Schritt: Wir können die gesamte Gleichung durch $U$ teilen und erhalten Formel für die Reihenschaltung von Widerständen:
\[ \boxed{\frac{1}{R_{ges}} = \frac{1}{R_1} + \frac{1}{R_2}} \]
Analog kann man sich überlegen, dass für mehrere Widerstände gilt:
\[ \boxed{\frac{1}{R_{ges}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} +\dots} \]
Zusammenfassung
Reihenschaltung von Widerständen
Die einzelnen Widerstände addieren sich zum Gesamtwiderstand.
Es gilt:
\[\boxed{R_{ges} = R_1+ R_2}\]
bzw.
\[\boxed{R_{ges} = R_1+ R_2+R_3+\dots}\]
Parallelschaltung von Widerständen
Die Kehrwerte der einzelnen Widerstände addieren sich zum Kehrwert des Gesamtwiderstands.
Es gilt:
\[ \boxed{\frac{1}{R_{ges}} = \frac{1}{R_1} + \frac{1}{R_2}} \]
bzw.
\[ \boxed{\frac{1}{R_{ges}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} +\dots} \]
Durch geschickte Kombination der existierenden Widerstände, können alle Widerstände ersetzt werden. Aus diesem Grund spricht man statt von Gesamtwiderständen, auch manchmal von Gesamtwiderständen.
Beispiele
Beispiel zur Reihenschaltung von Widerständen

Der Gesamtwiderstand dieser Schaltung ist: \[R_{ges}=R_1+R_2+R_3=500\Omega+50\Omega+100\Omega= 650\Omega \]
Beispiel zur Parallelschaltung von Widerständen
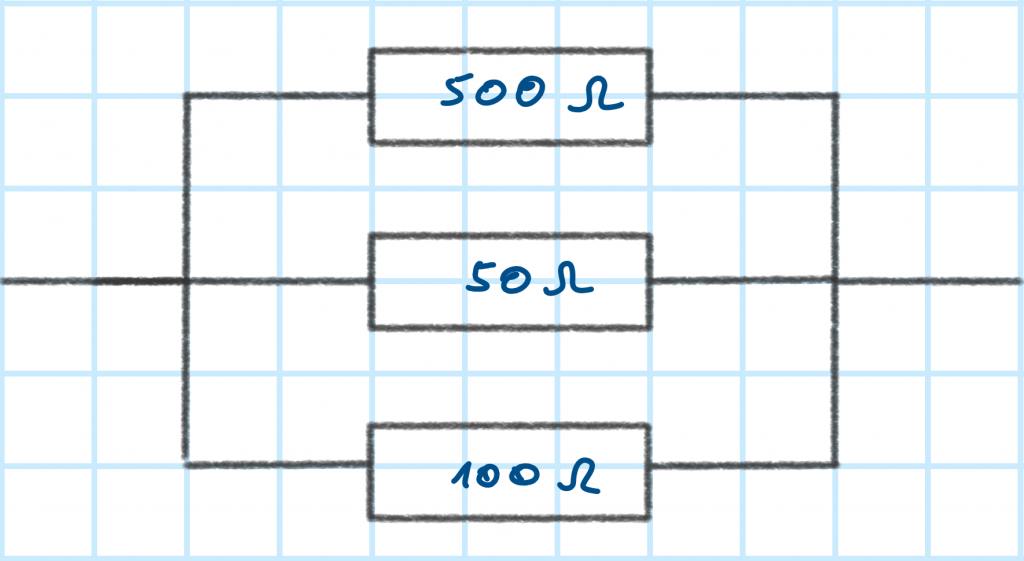
Der Gesamtwiderstand dieser Schaltung berechnet sich so:
Der Gesamtwiderstand der Parallelschaltung ist also $31,25\Omega$
Beispiel für eine Kombination aus Reihen- und Parallelschaltung
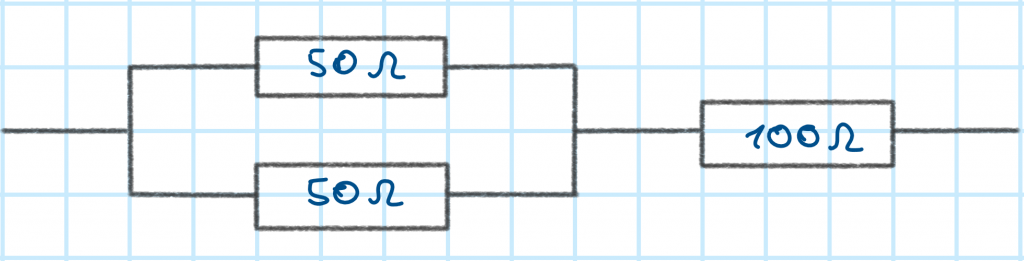
Um den Gesamt-bzw- Ersatzwiderstand einer Kombination von Reihen- und Parallelschaltung zu bestimmen, arbeitet man sich von innen nach außen vor. Das heißt, man berechnet zunächst den Ersatzwiderstand der kleinsten Reihen- bzw. Parallelschaltung. In obigem Beispiel betrachtet man also zunächst die Parallelschaltung der beiden $50\Omega$-Widerstände und arbeitet sich dann weiter nach außen fort. In diesem Beispiel ist es leicht und der Gesamtwiderstand der Parallelschaltung beträgt $25\Omega$. In anderen Fällen kann hier eine längere Rechnung nötig sein. Nun müssen noch die $100\Omega$ berücktsicht werden, die in Reihe geschaltet werden.
Der Gesamtwiderstand obiger Schaltung ist damit $125\Omega$ groß. Die dargestellte Kombination aus $100\Omega$ und $50\Omega$-Widerständen ist also eine mögliche Lösung des eingangs formulierten Problems.
Applet zur Berechnung des Gesamtwiderstands in einer Parallelschaltung
Wir haben festgestellt, dass die Berechnung des Ersatzwiderstands für eine Reihenschaltung sehr einfach ist. Da die Berechnung des Ersatzwiderstands einer Parallelschaltung allerdings duchaus unhandlich sein kann, stelle ich untentstehendes Applet vor. Mit dem Applet kann der Gesamtwiderstand einer Parallelschaltung von zwei, drei und vier Widerständen automatisiert berechnet werden.
