Bewegungen können mit Hilfe von Diagrammen dargestellt werden. Man verwendet dafür zwei Arten von Diagrammen:
Bei einem Zeit-Geschwindigkeits-Diagramm (auch t-v-Diagramm genannt) wird die Zeit auf der Rechtsachse und die Geschwindigkeit auf der Hochachse dargestellt.
Bei einem Zeit-Weg-Diagramm (auch t-s-Diagramm genannt) wird die Zeit auf der Rechtsachse und der Weg auf der Hochachse dargestellt.
Interpretation eines realen t-v-Diagramms
Mit Hilfe der App phyphox können z.B. die Daten aus dem GPS (Global Positioning System) eines gewöhnlichen Smartphones ausgelesen werden. Unten dargestellt sind die Daten, die während einer Autofahrt aufgenommen wurden:
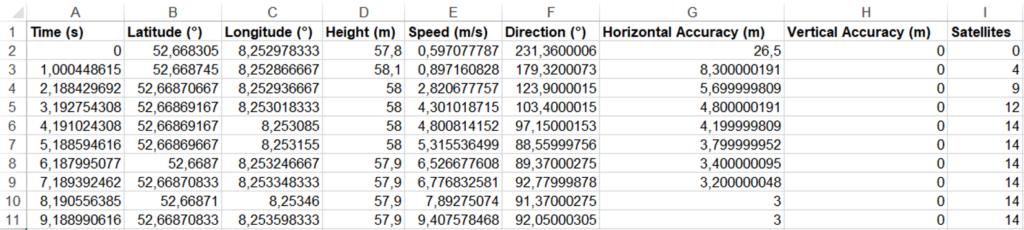
Mit Hilfe der Werte in der Spalte „Time (s)“ und „Speed (m/s)“ kann nun ein Zeit-Geschwindigkeits-Diagramm erstellt werden. Dazu wird die Zeit in Sekunden auf der Rechtsachse und die Geschwindigkeit in Meter pro Sekunde auf der Hochachse dargestellt:
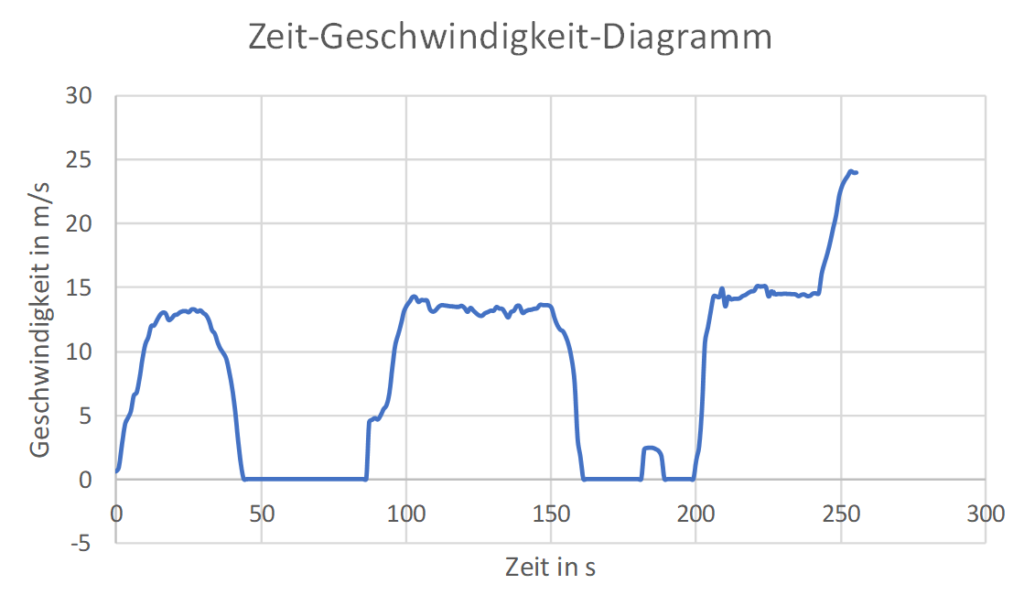
Aus diesem Diagramm lassen sich die verschiedensten Informationen entnehmen: Zu den Zeiten, in denen die Geschwindigkeit $0\dfrac{m}{s}$ beträgt, hat sich das Auto nicht bewegt – das Warten an einer Ampel ist naheliegend. Die kurze Geschwindigkeitsänderung bei $t\approx 180s$ kann als ein kurzes Anrollen an einer Ampel gedeutet werden, bevor wieder gehalten werden musste, um anderen Verkehrsteilnehmern Vorfahrt zu gewähren. Der starke Anstieg der Geschwindigkeit im Graphen bei $t\approx 240s$ lässt auf eine Änderung der Geschwindigkeitszone schließen. Tatsächlich befand sich an dieser Stelle das Ortsausgangsschild. Weiterhin lässt der der Graph an der Stelle $t\approx 80s$ auf einen langsam durchgeführten Gangwechsel schließen. Allein aufgrund des Diagramms ist also der Schluss naheliegend, dass das Auto kein Automatikgetriebe hat.
Im Zeit-Geschwindigkeit-Diagramm gilt:
- ein Anstieg des Graphen bedeutet eine Beschleunigung, also eine Erhöhung der Geschwindigkeit
- ein Fallen des Graphen bedeutet eine Bremsung, also eine Verminderung der Geschwindigkeit
- je steiler der Graph ansteigt/fällt, desto größer ist die Beschleunigung/Bremsung
- ist der Graph bei 0, so ist die Geschwindigkeit null und das betrachtete Objekt bewegt sich nicht
- verläuft der Graph parallel zur Zeitachse, bedeutet dies eine Beibehaltung der Geschwindigkeit. Es wird also weder beschleunigt noch gebremst.
Gegenüberstellung von t-s- und t-v-Diagrammen zweier Bewegungen
Wir betrachten das folgende t-s- bzw. t-v-Diagramm.
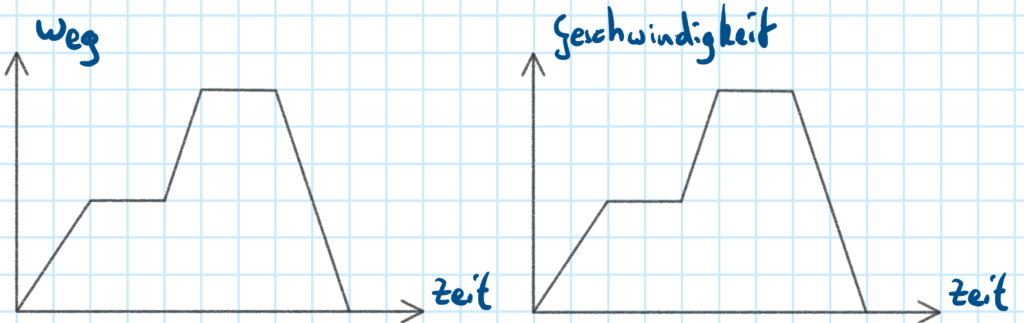
Achtung: Obwohl beide Diagramme gleich aussehen, sind die zugehörigen Bewegungen grundverschieden!
Beschreibung der im Zeit-Weg-Diagramm dargestellten Bewegung: Eine Person bewegt sich, bleibt dann stehen, läuft dann schneller als zuvor weiter, bleibt erneut stehen und bewegt sich dann zurück zum Ausgangsort.
Beschreibung der im Zeit-Geschwindigkeit-Diagramm dargestellten Bewegung: Eine Person beschleunigt, hält dann seine Geschwindigkeit, beschleunigt dann stärker als zuvor, hält erneut seine Geschwindigkeit und bremst dann bis zum Stillstand ab.
Im Zeit-Weg-Diagramm gilt:
- ein Anstieg des Graphen bedeutet eine Entfernung vom Ausgangsort
- ein Fallen des Graphen bedeutet eine Annäherung an den Ausgangsort.
- je steiler der Graph steigt, desto schneller entfernt sich das Objekt vom Ausgangsort, desto höher ist also die Geschwindigkeit
- je steiler der Graph fällt, desto schneller nähert sich das Objekt dem Ausgangsort, desto höher ist also die Geschwindigkeit
- ist der Graph bei 0, so ist das Objekt am Ausgangsort.
- verläuft der Graph parallel zur Zeitachse, bedeutet dies eine Stehenbleiben. Es findet keine Bewegung statt.
Man kann aus einem Zeit-Weg-Diagramm auch die Geschwindigkeit ermitteln.
