Als gleichförmige Bewegung wird eine Bewegung bezeichnet, bei der die Geschwindigkeit immer konstant ist. Wir untersuchen eine solche Bewegung mit Hilfe eines Fernautos, welches seine Geschwindigkeit immer beibehält.
Um die gleichförmige Bewegung näher untersuchen zu können, starten wir das Auto und messen alle 0,5m mit einer Stoppuhr die Zeit. Dabei erhalten wir die folgenden Messwerte:
| Weg s in Meter | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 |
| Zeit t in Sekunden | 1,3 | 3,4 | 4,1 | 5,9 | 7,1 | 8 | 9,5 | 10,9 | 12 | 13 |
Aus diesen Messwerten lässt sich das folgende Zeit-Weg-Diagramm erstellen.
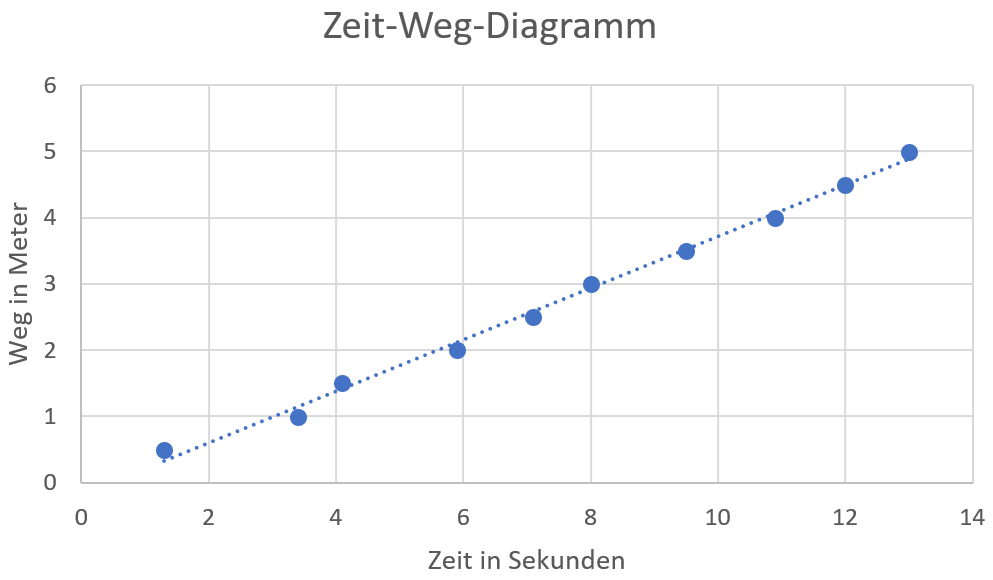
Das Diagramm legt den Schluss nahe, dass die Messwerte alle auf einer Geraden liegen. Dass dies nicht exakt der Fall ist, liegt vermutlich an einer ungenauen Messung. Die eingezeichnete Ausgleichsgerade ist dabei eine Möglichkeit, den Einfluss dieser Messungenauigkeiten zu minimieren. Die Ausgleichsgerade wurde so durch die Messwerte gelegt, dass möglichst viele Messwerte auf der Geraden liegen und weiterhin in etwa gleich viele Punkte ober- wie unterhalb der Geraden liegen.
Mathematisch gesprochen können wir festhalten: es gibt einen proportionalen Zusammenhang zwischen der Zeit und dem zurückgelegten Weg. Das bedeutet, dass eine Verdopplung der Zeit auch eine Verdopplung des zurückgelegten Wegs bedeutet. Das passt!
Gilt ein proportionaler Zusammenhang, so kann immer auch eine Proportionalitätskonstante bestimmt werden, in diesem Fall wäre das der Quotient $\dfrac{s}{t}$. Wir ergänzen obige Tabelle:
| Weg s in Meter | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 |
| Zeit t in Sekunden | 1,3 | 3,4 | 4,1 | 5,9 | 7,1 | 8 | 9,5 | 10,9 | 12 | 13 |
| $\dfrac{s}{t}$ in $\dfrac{m}{s}$ (gerundet) | 0,38 | 0,29 | 0,37 | 0,34 | 0,35 | 0,38 | 0,37 | 0,37 | 0,38 | 0,38 |
Wir erkennen: Näherungsweise ist der Quotient $\dfrac{s}{t}$ immer gleich. Ein Ausreißer z.B. beim Wert für $t=1s$ kann als Messungenauigkeit interpretiert werden; auch im obigen t-s-Diagramm liegt der Messwert für $t=1s$ neben der Ausgleichsgerade.
Wir deuten den Quotienten $\dfrac{s}{t}$ physikalisch als Geschwindigkeit der Bewegung. Unser Fernauto bewegte sich in unserem Versuch also mit etwa $0,37 \dfrac{m}{s}$. Das Auto bewegt sich also in jeder Sekunde etwa 37cm weiter nach vorne.
Wir halten fest:
Die Geschwindigkeit einer gleichförmigen Bewegung wird definiert als \[ \text{Geschwindigkeit} = \dfrac{\text{zurückgelegter Weg}}{\text{benötigte Zeit}} \] oder mit Formelzeichen: \[ v= \dfrac{s}{t} \]
