Mit Hilfe von Transformatoren kann die elektrische Spannung bzw. die elektrische Stromstärke hoch- bzw. runtergeregelt werden. Beispielsweise haben die meisten Handyakkus eine Spannung in der Größenordnung von 5V. Das normale Hausnetz hat jedoch eine Spannung von etwa 230V. Würde man die Spannung des Hausnetzes nicht zuvor durch entsprechende Maßnahmen verringern, würde der Akku des Handys zerstört werden. Mit Hilfe eines Transformators könnte man also die Spannung von 230V auf 5V herunterregeln.
Man sagt auch, dass die Spannung bzw. Stromstärke transformiert wird – daher der Name Transformator (kurz: Trafo).
Transformatoren können überall da Anwendung finden, wo die vorhandene Quellspannung (z.B. die Spannung im Hausnetz) zu groß für einen bestimmten Einsatzzweck ist (z.B. das Laden deines Handyakkus). Transformatoren werden auch benutzt, um die Spannung vor oder nach Hochspannungsleitungen herauf- oder herunterzutransformieren.
Aufbau und Funktionsweise eines Transformators
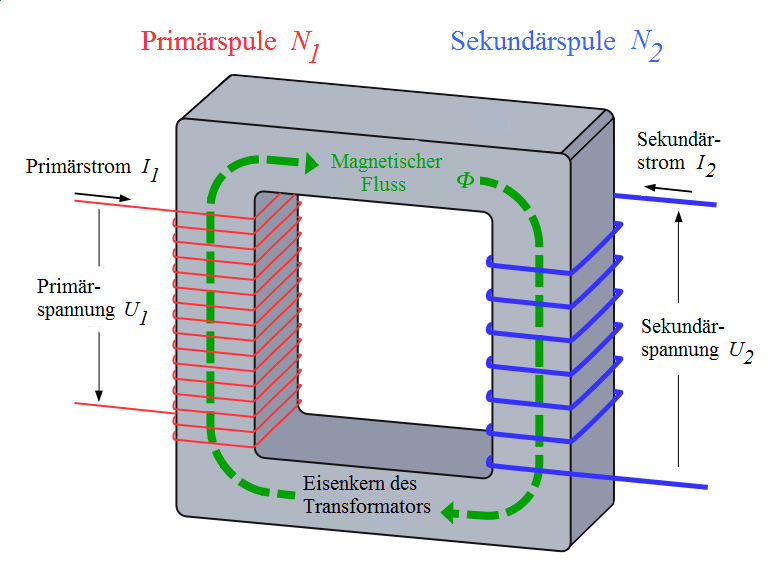
Ein Transformator besteht aus zwei Spulen mit verschiedenen Windungszahlen, die auf einen Eisenkern positioniert werden.
Wir erklären das Funktionsprinzip des Transformators Schritt für Schritt:
Fließt Strom durch eine Spule, so entsteht ein magnetisches Feld um diese Spule herum – das ist das Grundprinzip eines Elektromagneten. Legen wir an die Primärspule eine Wechselspannung an, bedeutet das, dass sich die Richtung des Stroms in der Primärspule ständig ändert. Dies wiederum hat zur Folge, dass sich auch das Magnetfeld um die Primärspule ständig ändert.
Der folgende Schritt im Funktionsprinzip des Transformators basiert auf Induktion. Induktion beschreibt dabei – vereinfacht ausgedrückt – den Effekt, dass z.B. in einer Spule ein Stromfluss entsteht, wenn sich das Magnetfeld, in dem sich die Spule befindet, verändert.
Durch das sich verändernde Magnetfeld der Primärspule wird in der Sekundärspule eine Spannung induziert. Da sich das Magnetfeld der Primärspule ständig verändert (und dabei mal zunimmt und mal abnimmt) ändert sich auch die Spannung in der Sekundärspule ständig – es wird also auch wieder eine Wechselspannung induziert.
Folglich funktioniert der Transformator nur dann, wenn an der Primärspule eine Wechselspannung angelegt wird. Würde man die Primärspule an eine Gleichstromquelle anschließen, würde zwar um die Primärspule ein Magnetfeld entstehen, aber da sich dieses nicht verändert, wird keine Spannung in der Sekundärspule entstehen (außer beim Ein- und Ausschalten der Spannung an der Primärspule).
Durch den Transformator wird dabei abhängig von dem Verhältnis der Windungszahlen der verwendeten Spulen die Spannung erhöht bzw. erniedrigt und entsprechend die Stromstärke erniedrigt bzw. erhöht.
Mathematische Zusammenhänge am Transformator
Spannung am Transformator
Untersucht man die Spannungen $U_1$ und $U_2$ der Primär- bzw. Sekundärspule für verschiedene Windungszahlen stößt man z.B. auf das folgende Ergebnis:
| Windungszahl der Primärspule | Windungszahl der Sekundärspule | Spannung an der Primärspule | Spannung an der Sekundärspule |
|---|---|---|---|
| 500 | 1000 | 6 V | 12 V |
| 500 | 2000 | 6 V | 24 V |
| 500 | 2000 | 12 V | 48 V |
| 1000 | 2000 | 12 V | 24 V |
| 1000 | 500 | 6 V | 3 V |
| 2000 | 500 | 6 V | 1,5 V |
Wir halten folgende Erkenntnisse fest:
- Ist die Windungszahl der Sekundärspule größer als die Windungszahl der Primärspule ist auch die Sekundärspannung größer als die Primärspannung.
- Ist die Windungszahl der Sekundärspule kleiner als die Windungszahl der Primärspule ist auch die Sekundärspannung kleiner als die Primärspannung.
- Das Verhältnis der Windungszahlen $N_2/N_1$ gibt an, mit welchen Faktor die Spannung verändert wird.
- Das Verhältnis der Windungszahlen $N_2/N_1$ entspricht dem Verhältnis der Spannungen $U_2/U_1$.
Für den Zusammenhang zwischen den Spannungen und den Windungszahlen am Transformator können wir festhalten:
\begin{equation} \boxed{ \dfrac{N_2}{N_1} = \dfrac{U_2}{U_1} \text{ oder auch } \dfrac{N_1}{N_2} = \dfrac{U_1}{U_2} } \end{equation}
Stromstärke am Transformator
Untersucht man die Stromstärken $I_1$ und $I_2$ der Primär- bzw. Sekundärspule für verschiedene Windungszahlen stößt man z.B. auf das folgende Ergebnis:
| Windungszahl der Primärspule | Windungszahl der Sekundärspule | Spannung an der Primärspule | Spannung an der Sekundärspule |
|---|---|---|---|
| 500 | 1000 | 1 A | 0,5 A |
| 500 | 2000 | 1 A | 0,25 A |
| 500 | 2000 | 2 A | 0,5 A |
| 1000 | 2000 | 2 A | 1 A |
| 1000 | 500 | 1 A | 2 A |
| 2000 | 500 | 1 A | 4 A |
Wir halten folgende Erkenntnisse fest:
- Ist die Windungszahl der Sekundärspule größer als die Windungszahl der Primärspule ist die Sekundärstromstärke kleiner als die Primärspannung.
- Ist die Windungszahl der Sekundärspule kleiner als die Windungszahl der Primärspule ist die Sekundärstromstärke größer als die Primärspannung.
- Das Verhältnis der Windungszahlen $N_1/N_2$ gibt an, mit welchen Faktor die Stromstärke verändert wird.
- Das Verhältnis der Windungszahlen $N_2/N_1$ entspricht dem Verhältnis der Stromstärken $I_1/I_2$
Für den Zusammenhang zwischen den Stromstärken und den Windungszahlen am Transformator können wir festhalten:
\begin{equation} \boxed{\dfrac{N_2}{N_1} = \dfrac{I_1}{I_2} \text{ oder auch } \dfrac{N_1}{N_2} = \dfrac{I_2}{I_1} } \end{equation}
Spannung und Stromstärke am Transformator
Entscheidend für die Veränderung der Spannung bzw. der Stromstärke ist jeweils das Verhältnis der Windungszahlen $N_1/N_2$. Wichtig zu beachten ist, dass der Transformator dabei entweder die Spannung oder die Stromstärke erhöhen bzw. niedrigen kann. Die jeweils andere Komponente wird sich dann im gleichen Maße erniedrigen bzw. erhöhen.
Wir betrachten einen Transformator mit $N_1=500$ und $N_2=10 000$. Das Verhältnis der Windungszahlen ist also 20. Die Spannung wird mit diesem Transformator also mit dem Faktor 20 multipliziert, während die Stromstärke auf $1/20$ absinken wird. Vertauscht man die Rollen von Primär- und Sekundärspule wird entsprechend die Spannung auf $1/20$ absinken und die Stromstärke wird mit dem Faktor 20 multipliziert.
Der Energieerhaltungssatz bleibt dementsprechend erfüllt und die Leistung ändert sich – im Idealfall – nicht, die Leistung $P= U\cdot I$ ist also im Primär- und im Sekundärkreis gleich.
Experimente am Transformator
Sicherheitshinweis: Führe niemals eigenständig Transformatorexperimente durch. Die dabei entstehenden Spannungen können schnell lebensgefährlich werden.
Lichtbogen am Transformator
Verwenden wir beispielsweise eine Primärspule mit 500 Windungen und eine Sekundärspule mit 23000 Windungen, so können wir die Spannung an der Sekundärspule berechnen:
Es ist:
\begin{align*} \frac{N_2}{N_1} &= \frac{U_2}{U_1} \\ \frac{23000}{500} &= \frac{U_2}{230 V} \\ 46 &= \frac{U_2}{230 V} \\ U_2 &= 46\cdot 230 V \\ U_2 &= 10 580 V \end{align*}
Bei diesem Versuch entsteht eine Sekundärspannung, die mit über 10 000 V lebensgefährlich sein kann. Diese Spannung ist sogar so hoch, dass die Luft leitend wird – es können Blitze entstehen. Dies kann man zum Beispiel in dem folgendem Experiment sehen.
Der Transformator als Schweißtransformator
Im vorigen Experiment haben wir mit Hilfe eines Transformators eine extrem hohe Spannung erzeugt. Im nächsten Versuch erzeugen wir mit Hilfe eines Transformators eine extrem hohe Stromstärke. Dazu verwenden wir eine Primärspule mit 500 und eine Sekundärspule mit 5 Windungen. Durch den Primärstromkreis fließt eine Stromstärke von 2,3A.
Es ergibt sich als Sekundärstromstärke:
\begin{align*} \frac{N_1}{N_2} &= \frac{I_2}{I_1} \\ \frac{500}{5} &= \frac{I_2}{2,3 A} \\ 100 &= \frac{I_2}{2,3 A} \\ I_2 &= 100\cdot 2,3 A\\ I_2 &= 230A \end{align*}
Bei diesem Versuch entsteht also eine Stromstärke von 230 Ampere. Diese Stromstärke ist so hoch, dass sie, wenn sie z.B. durch einen Nagel fließt, diesen zum Schmelzen bringen kann. Diesen Effekt kann man z.B. in dem folgendem Experiment sehen, indem der Transformator zum Schweißen benutzt wird:
Energieübertragung mit Hochspannungsleitungen
Warum verwendet man eigentlich Hochspannungsleitungen?
Die Energieübertragung von den Kraftwerken erfolgt in der Regel so, dass die Spannung am Kraftwerk in einem Umspannwerk (vorstellbar als riesiger Transformator) deutlich erhöht wird – bei Überlandleitungen werden oft 110 kV, also 110 000 V verwendet – und dann im Stadtgebiet angekommen an einem weiteren Umspannwerk wieder heruntertransformiert wird.
Doch warum erhöht man die Spannung für den Übertragungsweg?
Eine einfache Erklärung dafür erfolgt mit Hilfe des Zusammenhangs $P=U\cdot I$. Die zu übertragende Leistung P können wir uns als sehr groß vorstellen, da mit dieser Leistung z.B. eine ganze Stadt versorgt werden muss.
Betrachten wir die Extremfälle gibt es nun zwei Optionen, wie wir auf eine große Leistung kommen: Entweder wir haben eine große Spannung und eine kleine Stromstärke oder wir haben eine kleine Spannung und eine große Stromstärke. Das Problem einer zu großen Stromstärke haben wir z.B. beim Experiment zum Schweißtransformator gesehen: die Leitungen würden zu glühen beginnen oder müssten extrem dick – und damit teuer – sein. Die Verluste bei der Übertragung wären folglich riesig, wenn Überlandleitungen mit einer Spannung von z.B. 230 V arbeiten würden.