Aus einem Zeit-Weg-Diagramm lässt sich ebenfalls eine Information über die Geschwindigkeit gewinnen – diese ist jedoch nicht unmittelbar abzulesen. Wir betrachten als Beispiel das folgende t-s-Diagramm:
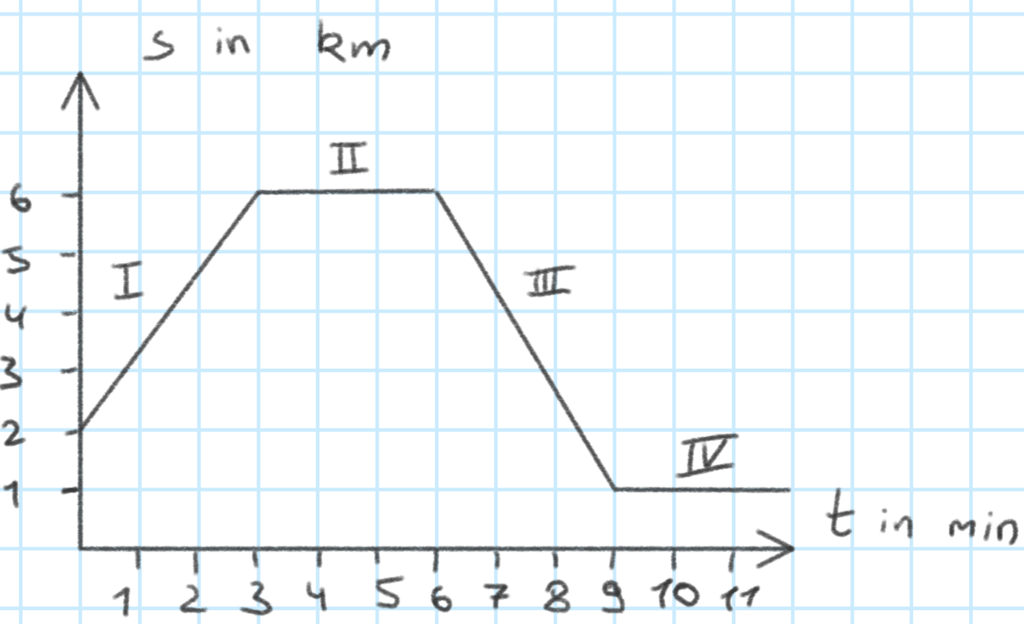
Zunächst interpretieren wir das t-s-Diagramm: Die Bewegung im Beispiel kann in 4 Abschnitte unterteilt werden. In all diesen Abschnitten ist die Bewegung jeweils gleichförmig, erfolgt also mit gleichbleibender Geschwindigkeit. Dies ist daran zu erkennen, dass alle Abschnitte im t-s-Diagramm linear sind.
In Abschnitt I startet die Bewegung in Abstand von 2km vom festgelegten Nullpunkt und bewegt sich dann innerhalb von 3 Minuten 4km vorwärts. Dann bleibt das Objekt in Abschnitt II für 3 Minuten an seiner Position. In Abschnit III bewegt sich das Objekt innerhalb von 4 Minuten um 5km zurück und bleibt dann in Abschnitt IV wieder für 3 Minuten an diesem Ort. Die Bewegungsrichtungen in den Abschnitten I und III sind also entgegengesetzt.
Um nun die Geschwindigkeiten in den einzelnen Abschnitten zu bestimmen, verwendet man die Formel für die Geschwindigkeit einer gleichförmigen Bewegung und liest die Werte aus dem Diagramm ab.
In Abschnitt I ändert sich der Ort des Objektes wie beschrieben innerhalb von 3 Minuten um 4km. Beim Ablesen der Werte kann dabei auch ein Steigungsdreieck helfen:
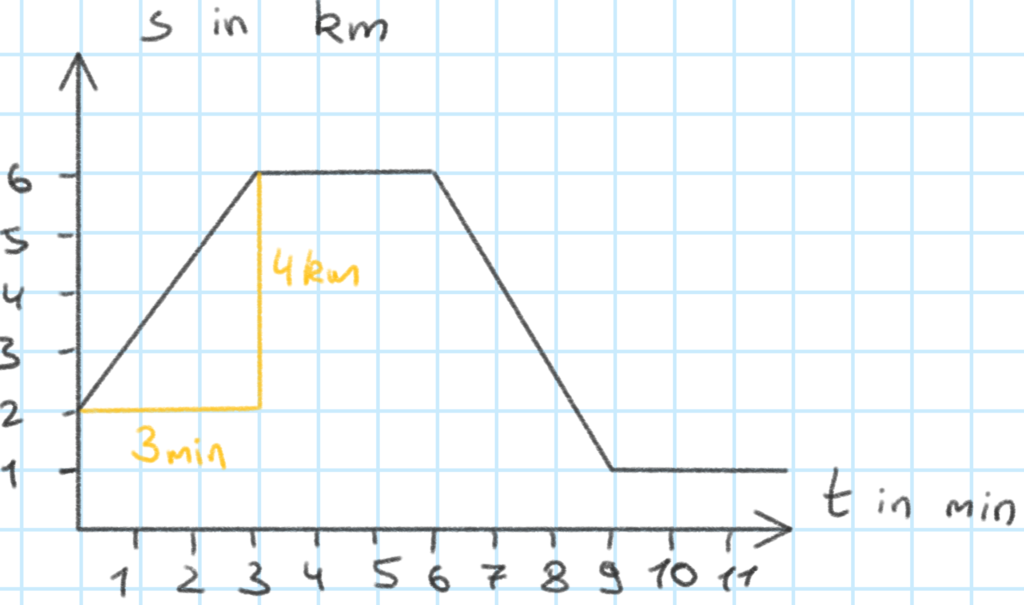
Die Geschwindigkeit in Abschnitt I ist also:
\[ v= \dfrac{s}{t}= \dfrac{4 km}{3 min} = 1,\overline{3} \dfrac{km}{min} = 80 \dfrac{km}{h} \]
In Abschnitt II muss nicht großartig gerechnet werden: Da der Graph im t-s-Diagramm horizontal verläuft, ändert sich der Ort nicht, folglich steht das Objekt und seine Geschwindigkeit ist $0 \dfrac{km}{h}$
In Abschnitt 3 kann wiederum das Steigungsdreieck helfen:
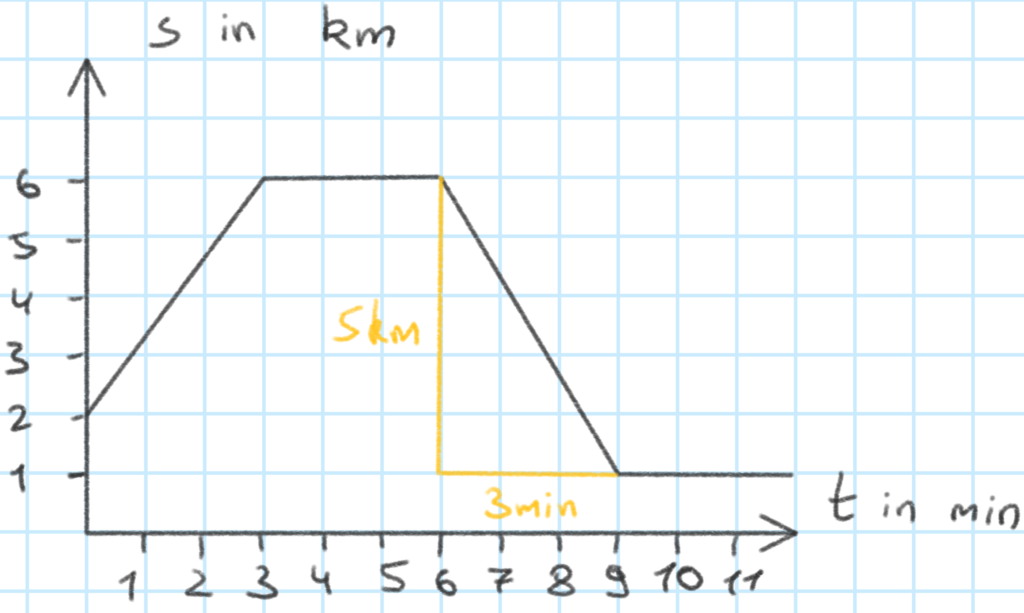
Innerhalb von 3 Minuten bewegt sich das Objekt also um 5km. Also ist die Geschwindigkeit in Abschnitt III:
\[ v= \dfrac{s}{t}= \dfrac{5 km}{3 min} = 1,\overline{6} \dfrac{km}{min} = 100 \dfrac{km}{h} \]
Wichtig ist jedoch festzuhalten, dass die Bewegungen in Abschnitt I und III entgegengesetzt sind. Daher wird die Geschwindigkeit in Abschnitt III daher auch mit $v=- 100 \dfrac{km}{h}$ angegeben. Das Minus soll genau diese entgegengesetzte Bewegung verdeutlichen.
Für Abschnitt IV gilt wiederum die selbe Überlegung wie in Abschnitt II und die Geschwindigkeit ist $0 \dfrac{km}{h}$
Ermittlung der Geschwindigkeit aus einem t-s-Diagramm allgemein
Möchte man den gerade durchgeführten Ansatz allgemein formulieren, so muss man sich für die Berechnung der Geschwindigkeit eines Abschnittes auf zwei Zeit- und zwei Weg-Werte beziehen. Daher benutzt man nun die Abkürzungen $t_1$ und $t_2$ sowie $s_1$ und $s_2$:
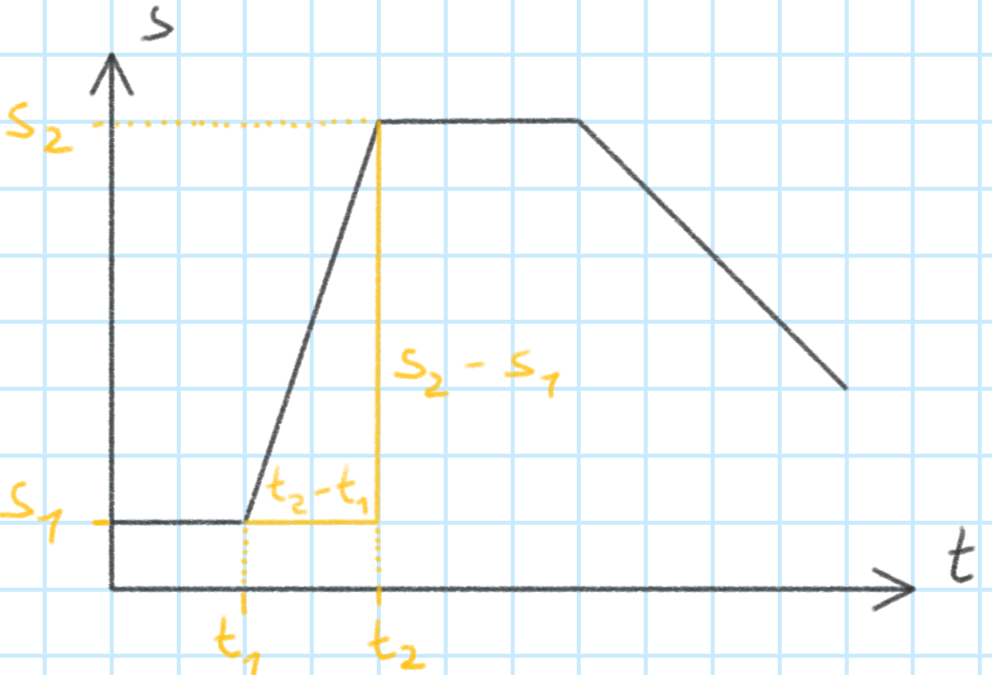
Man kann nun die Geschwindigkeit v berechnen mit $ v= \dfrac{s}{t}= \dfrac{s_2-s_1}{t_2-t_1} $.
Beziehen wir beispielsweise diese allgemeine Formulierung auf Abschnitt III des vorherigen Beispiels, so ergibt sich:
\[ v= \dfrac{s}{t}=\dfrac{1km – 6km}{9min – 6min} = \dfrac{-5km}{3 min} = -1,\overline{6} \dfrac{km}{min} = -100 \dfrac{km}{h} \]
Dieser Ansatz erklärt nun also auch formal das bereits vorher angesprochene negative Vorzeichen.
