Wir untersuchen, wie sich die Temperatur von Wasser bei Energiezufuhr verändert. Dafür verwenden wir ein modernes Messwerterfassungssystem (CASSY), um die Temperaturveränderung in einem Wasserkocher mit 1l Wasser zu beobachten. Die Messwerterfassung erspart uns dabei ein händisches Ablesen der Temperatur. Im Versuch verwenden wir einen Wasserkocher mit einer elektrischen Leistung von 1750 Watt und nehmen dabei das folgende Zeit-Temperatur-Diagramm auf.
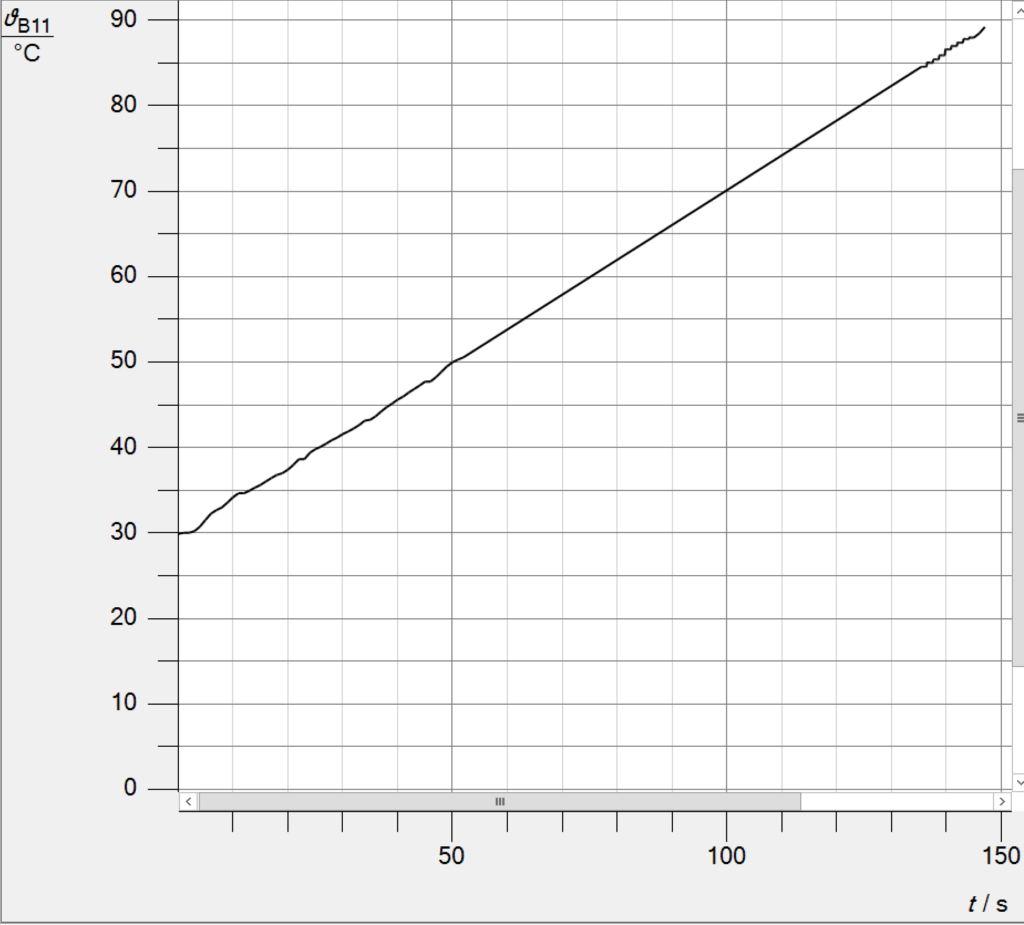
Dem Zeit-Temperatur-Diagramm zu entnehmen ist, dass die Temperatur im Bereich von 30°C bis etwa 90°C annähernd linear ansteigt.
Bestimmung der spezifischen Wärmekapazität von Wasser – einfache Methode
Im obigen Diagramm kann man gut ablesen, dass die Temperatur nach 50s etwa 50°C und nach 100s etwa 70°C beträgt. Die Energie, die in diesen 50s an das Wasser übertragen wurde, lässt sich berechnen:
\[ E = P\cdot t = 1750 W \cdot 50s = 87500 J \]
Also werden 87 500 J benötigt, um 1l Wasser um 20°C zu erwärmen. Damit ist dann die benötigte Energie für die Erwärmung von 1g Wasser um 1°C:
\[ c = \dfrac{87500 J}{1000g \dot 20°C } = 4,375 \dfrac{J}{g\cdot °C} \]
Dieser Wert wird als spezifische Wärmekapazität bezeichnet und liegt sehr nahe am Literaturwert für die spezifische Wärmekapazität von Wasser $c_\text{Wasser} = 4,19 \dfrac{J}{g\cdot °C} $. Man benötigt also
Die früher gebräuchliche Standardeinheit der Energie in der Physik war die Einheit Kalorie (cal): Eine Kalorie wurde definiert als die Energiemenge, die man benötigt, um 1g Wasser um 1°c zu erwärmen. Eine Kilokalorie (kcal) ist entsprechend die Energiemenge, die man benötigt, um 1kg Wasser um 1°C zu erwärmen.
Energie Temperatur Gleichung
Die Erkenntnisse dieses Versuchs lassen sich in der Energie Temperatur Gleichung zusammenfassen:
Die Energie Temperatur Gleichung lautet \[ \boxed{E = c\cdot m \cdot \Delta\vartheta} \] Dabei ist \begin{align*} E &\dots \text {die zugeführte bzw. benötigte Energie in J} \\ c &\dots \text{die spezifische Wärmekapazität in $\dfrac{J}{g\cdot °C}$} \\ m &\dots \text{die Masse in g } \\ \Delta\vartheta &\dots \text{die Temperaturveränderung in °C} \end{align*}
Bestimmung der spezifischen Wärmekapazität von Wasser – Profivariante
Eine Kritik an der vorhergehenden Herangehensweise könnte sein: Man hat nur 2 Messwerte benutzt. Nachdem das Cassy zuvor etliche Messwerte aufgenommen hat, um das Zeit-Temperatur-Diagramm zu erstellen, haben wir uns in der bisherigen Auswertung nur auf die beiden Wertepaare $(50s|50°C)$ und $(100s|70°C)$ gestützt. Eine lineare Regression ist eine mathematische Möglichkeit, alle Messwerte zu berücksichtigen und so den Einfluss von Messungenauigkeiten zu minimieren.
Eine solche lineare Regression liefert hier das Ergebnis $\Delta\vartheta = 0,406 \dfrac{°C}{s}\cdot t$. Wir vergleichen dies mit $\Delta\vartheta$ aus der Energie Temperatur Gleichung:
\begin{align*} E &= c\cdot m \cdot \Delta\vartheta \\ \Delta\vartheta &= \dfrac{E}{c\cdot m} = \dfrac{P\cdot t}{c\cdot m} = \dfrac{P}{c\cdot m} \cdot t \end{align*}
Folglich müssen also $0,406 \dfrac{°C}{s}$ und $\dfrac{P}{c\cdot m}$ übereinstimmen. Also gilt:
\begin{align*} 0,406 \dfrac{°C}{s} & = \dfrac{P}{c\cdot m} \\ c &= \dfrac{P}{0,406 \dfrac{°C}{s}\cdot m } \\ c &= \dfrac{1750 W}{0,406 \dfrac{°C}{s}\cdot 1000g } \\ c& \approx 4,31 \dfrac{J}{g\cdot °C} \end{align*}
Mit Hilfe der linearen Regression konnten wir also für die spezifische Wärmekapazität von Wasser einen Wert bestimmen der noch näher am Literaturwert liegt.
Applet zu Berechnungen mit der Energie Temperatur Gleichung
Mit dem folgendem Applet lassen sich die grundlegenden Berechnungen mit der Energie Temperatur Gleichung durchführen.
